
Standard error decreases when sample size increases – as the sample size gets closer to the true size of the population, the sample means cluster more and more around the true population mean. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions. the variance of the population, increases. Standard error increases when standard deviation, i.e. Add 1 / sample size and 1 / population size. And you should notice it has decreased quite a bit from the standard deviation 1.7077 we had for a sample of size n 1. For example, a sample of heights of everyone in a town might have observations of 60 inches, 64 inches, 62 inches, 70 inches and 68 inches and the town is known to have a normal height distribution and standard deviation of 4 inches in its heights. This is our standard error, the standard deviation of our sampling distribution for the mean of two dice. Standard error can be calculated using the formula below, where σ represents standard deviation and n represents sample size. In Cell G3, I calculated the standard deviation of the sample averages, 1.21628. the means are more spread out, it becomes more likely that any given mean is an inaccurate representation of the true population mean. The standard error tells you how accurate the mean of any given sample from that population is likely to be compared to the true population mean. (a) Construct and interpret a 99 confidence interval for the difference in the true proportions of men and women aged 19. (Ref: ) The survey found that 986 of the men and 923 of the women lived in their parents’ home. the standard deviation of sample means, is called the standard error. A random sample by the National Institutes of Health included 2253 men and 2629 women who were between the age of 19 and 25. The standard deviation of this distribution, i.e. It is a measure of the extent to which data varies from the mean. Standard Deviation is square root of variance. Where is Mean, N is the total number of elements or frequency of distribution. If you take enough samples from a population, the means will be arranged into a distribution around the true population mean. First, calculate the deviations of each data point from the mean, and square the result of each: variance 4. Because of this, you are likely to end up with slightly different sets of values with slightly different means each time. When you are conducting research, you often only collect data of a small sample of the whole population. Divide the sum by the number of values in the data set.For each value, find the square of this distance.For each value, find its distance to the mean.The steps in calculating the standard deviation are as follows: It can, however, be done using the formula below, where x represents a value in a data set, μ represents the mean of the data set and N represents the number of values in the data set.
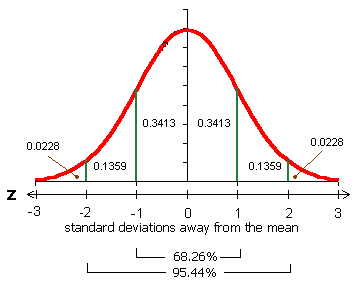
Standard deviation is rarely calculated by hand. In any distribution, about 95% of values will be within 2 standard deviations of the mean. It is a measure of how far each observed value is from the mean.

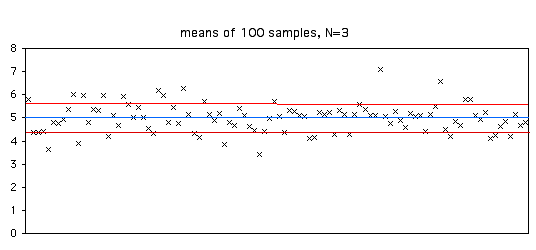
However, the error with a sample of size \(n=5\) is on the average smaller than with a sample of size \(n= 2\).Standard deviation tells you how spread out the data is. Population Mean 9 10 11 12 13 14 15 16 17 18 2 5 Sample SizeĪgain, we see that using the sample mean to estimate population mean involves sampling error.
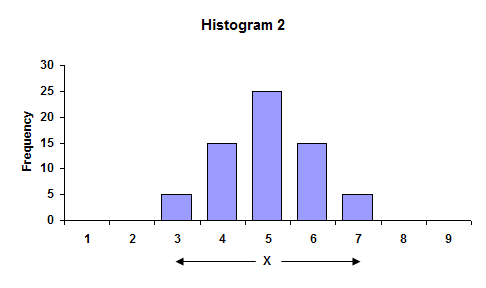
The following dot plots show the distribution of the sample means corresponding to sample sizes of \(n=2\) and of \(n=5\). Now that we have the sampling distribution of the sample mean, we can calculate the mean of all the sample means. (In some other examples, it may happen that the sample mean can never be the same value as the population mean.) When using the sample mean to estimate the population mean, some possible error will be involved since the sample mean is random. One can see that the chance that the sample mean is exactly the population mean is only 1 in 15, very small. It might be helpful to graph these values. It is also worth noting that the sum of all the probabilities equals 1. The formula is true as there are a total of 16 samples obtained by sampling with replacement. The table is the probability table for the sample mean and it is the sampling distribution of the sample mean weights of the pumpkins when the sample size is 2. In my calculation, I used the formulas for the population standard deviation and not the sample standard deviation. We can combine all of the values and create a table of the possible values and their respective probabilities.


 0 kommentar(er)
0 kommentar(er)
